重写 500 Lines or Less 项目 - FlowShop
概述
本文章是 重写 500 Lines or Less 系列的其中一篇,目标是重写 500 Lines or Less 系列的原有项目:A Flow Shop Scheduler。
背景
FlowShop 是一个关于工作调度的算法问题,主要来自工厂的流水线,为了便于建立模型和计算进行了某种程度的简化。其基本场景是一个工作车间,假定:
- 该车间存在m台机器;
- 完成一项生产任务称为一个作业(
Job),它由m个任务(Task)组成,其中每个任务需要依次在机器i上完成; - 一台机器上同时只能运行一个任务;
- 同一个作业(
Job)的各项任务(Task)必须串行执行。也就是说,在任务i-1完成之前,任务i必须等待;
在满足以上条件的前提下,各个作业调度到哪台机器可以灵活排列,目的是在众多可能的组合中找到一个最优的排列,使得所有作业运行消耗的总时间尽可能短。从理论上讲,我们可以通过穷举所有可能的组合来找到这个最优解,但排列组合的数量非常巨大,全部计算往往是不切实际的。因此我们退而求其次,将目标设定为:在有限的时间范围内找到一个较为合理的组合方案。
这种算法可以称为“爬山”(hillclimbing)。在爬山时,我们会从某个位置出发,只要不断往高处走,最后总能到达(一定范围内的)最高点。该算法的思想也是类似的:从某个随机排列开始,查找与它“相邻”的方案中结果更好的那些,再从这些方案触发继续搜索,直到找到最佳答案。
如果用一个示意图来表示该算法的原理,大概类似这样:
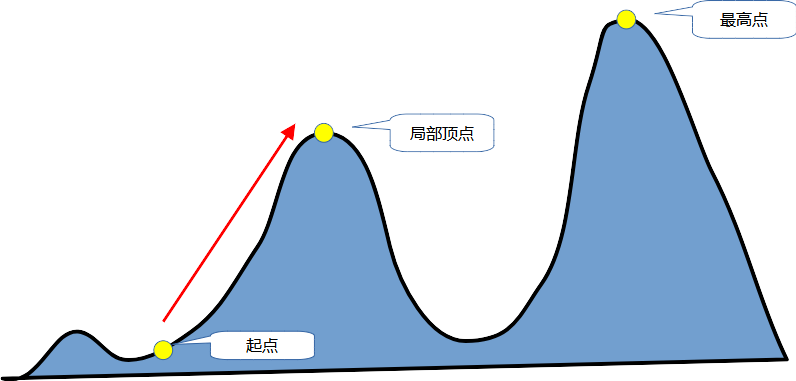
从图中可以看到,如果查找的方向只是“往上走”,那么我们未必能找到理论上的最佳结果,但一定可以找到特定范围内的最优解。当然,这个找不到的最优解只是一种可能性,我们无法预先知道它是否存在、以及会在什么地方。但是既然存在这种可能,就可以通过在算法中加入一定的随机性,让它不是只朝一个方向走,而是同时也探索其他可能的路径,从而加大找到最优解的概率。
了解了问题背景,现在来看一个具体实例,以便有一个更加直观的理解,并同时介绍计算过程中会用到的一些术语。
案例和术语
原文的代码库为我们提供了一些作业的案例,你可以在该项目的 instances 目录下找到它们。比如,instances/tai20_5.txt文件中第一个例子是这样的:
number of jobs, number of machines, initial seed, upper bound and lower bound :
20 5 873654221 1278 1232
processing times :
54 83 15 71 77 36 53 38 27 87 76 91 14 29 12 77 32 87 68 94
79 3 11 99 56 70 99 60 5 56 3 61 73 75 47 14 21 86 5 77
16 89 49 15 89 45 60 23 57 64 7 1 63 41 63 47 26 75 77 40
66 58 31 68 78 91 13 59 49 85 85 9 39 41 56 40 54 77 51 31
58 56 20 85 53 35 53 41 69 13 86 72 8 49 47 87 58 18 68 28
以上数字表明,该案例中共有 5 台机器,总共 20 个作业,(i,j) 位置的数字表示作业 j 中的任务 i 执行所需的时间。
当然,我们可以任意选择某个作业在哪台机器上执行,假定一种排列( permutation,代码中一般简写为perm)如下:
[14, 16, 13, 8, 7, 10, 12, 4, 2, 0, 18, 6, 15, 5, 17, 1, 3, 9, 19, 11]
该排列表明:序号为 14 的任务被安排到 0 号机器上执行,依次类推。为了和编程语言的规则保持一致,这些数字统一从0开始计数,以下如无特殊说明的话也都按照此原则表述。
当作业的排列顺序确定以后,我们就可以计算所有作业完成所需的总时间。在原文中将该时间称为 makespan,它等于最后一个任务的完成时间。
改写
原文代码时显然是基于 Python2 编写的,通过程序中对 print 的调用就可以很明白地看到。所以在尝试重写代码时,首要的目标就是将语言平台改为 Python3。
第二个目标是分步骤、逐步写完整个程序,而不是直接给出最终的代码。这个原则在本系列的各篇文章中已经多次强调,这里不再赘述。
在重写代码时,我尝试在风格上做出的另一个重大变化是:更多地使用面向对象式的风格,而不是像原代码那样大量使用原生数据结构和函数。之所以这么做,是因为在阅读原代码之后认识到:首先,本程序算法较为复杂,如果没有便于理解的名字,仅仅是通过下标访问数据,很不直观,容易对阅读造成困难;其次,部分代码出现了明显的数据“聚集”趋势,定义一个数据结构去统一管理接口,有助于分离职责,使得每个部分的作用更为清晰。
我本人并不是 OOP 的绝对信仰者,而是更倾向于实用主义;如果没有看到明确的好处,我并不会尝试用对象去封装每一个接口。不过对于该程序而言,我相信适当使用 OOP 是有好处的。当然,读者可以在对比两种代码风格以后得出自己的结论。
本文代码也添加了一定的单元测试来保证程序的正确性(原文代码并不包含单元测试)。略有遗憾的是,由于本文实现的是一种启发性算法,本身带有一定的不确定性,多次运行也可能得到略有差异的结果。因此,单元测试的作用仅能捕获到边界错误和部分逻辑问题,并不能保证结果一定是正确的。所以最基本的验证方法还是和原文类似:提供一个 dump() 方法(原文叫做 print_solution()),把输出结果和中间信息打印出来,用肉眼去确认结果是否正确。尽管输出内容看起来比较复杂,不过只要熟悉了其内容,还是很容易发现其中问题的。
源码
本文实现程序位于代码库的 flow_shop 目录下。按照本系列程序的一致规则,要想直接执行各个已完成的步骤,在根目录下的 main.py 找到相应的代码位置,取消注释并运行即可。
本程序的所有步骤只需要 Python3 即可,不需要其他额外的第三方库。原则上Python3.6 以上版本应该都可运行,但我只在 Python3.8.3 环境下完整测试过。如果读者发现版本兼容性问题的话,也欢迎来信或者发 issue 告知我。
以下分步骤来实现该程序。
实现
本文实现的程序将整个任务分解为6个步骤,逐步完整。这些步骤包括:
- 读取数据文件
- 计算指定任务序列的结果
- 实现策略(strategy)骨架
- 增加多种复杂策略
- 实现动态策略选择
- 通过缓存提高性能
接下来依次介绍各个步骤。
步骤0:读取文件
我们采用和原文一致的数据来源。这些数据位于 instances 目录下的各个文本文件中,其格式前面已经介绍过,现在不妨再回头看看其中的细节:
number of jobs, number of machines, initial seed, upper bound and lower bound :
20 5 873654221 1278 1232
processing times :
54 83 15 71 77 36 53 38 27 87 76 91 14 29 12 77 32 87 68 94
79 3 11 99 56 70 99 60 5 56 3 61 73 75 47 14 21 86 5 77
16 89 49 15 89 45 60 23 57 64 7 1 63 41 63 47 26 75 77 40
66 58 31 68 78 91 13 59 49 85 85 9 39 41 56 40 54 77 51 31
58 56 20 85 53 35 53 41 69 13 86 72 8 49 47 87 58 18 68 28
number of jobs, number of machines, initial seed, upper bound and lower bound :
核心的数据是一个空格分隔的数字矩阵,其前后的文字格式是固定的(那些额外的统计信息可以忽略不计)。但是最后一个矩阵后面不再有内容,为了方便统一护理,我们可以读取内容后自己再增加一行。
顺便说明一下,OOP的主要原则是每种事物应该有一个明确的名字。为了方便表述,我把上述包含多个作业、需要整体计算的矩阵数据称为一个批次(Batch)。从数据结构上看,一个 Batch 就是一个二维数组,对应到 Python 数据结构则是列表的列表。原文对此数据的叫法是 data,但我认为这个名称太过泛化而缺乏描述性。
读取数据是一个确定性工作,很合适用测试驱动:
class ReaderTest(TestCase):
def test_read_sample_batch(self):
batch = reader.read_sample_batch()
expected = [
[54, ...],
]
self.assertEqual(expected, batch)
为了方便起见,后续的实现和测试都使用第一个数据文件中的第一个 Batch, 代码中称为 sample batch。
SECTION_PREFIX = 'processing times :'
SECTION_SUFFIX = 'number of jobs, ...'
def read_file(file_name: str):
def parse_tasks(line):
return [int(x) for x in line.strip().split()]
def parse_batch(text):
return [parse_tasks(x) for x in text.split('\n') if x.strip()]
file_path = os.path.abspath(os.path.join(os.path.dirname(__file__), '../instances', file_name))
pattern = SECTION_PREFIX + r'([\d\s]+)' + SECTION_SUFFIX
with open(file_path, 'r') as f:
content = f.read() + '\n' + SECTION_SUFFIX
return [parse_batch(x) for x in re.findall(pattern, content)]
解析文件使用自顶向下的风格。为了不让代码主体过于复杂,将子任务分解成了两个内部函数。基本上,上述代码做了这些工作:
- 读取文件的所有行,并且为了让数据格式统一,在最后增加一个辅助行;
- 用正则表达式捕获矩阵部分的内容
- 对于每个捕获到的矩阵,将其解析为一个二维数组,也就是
Batch
为节约篇幅,列出的代码省略了部分过长的字符串。完整代码可以从 Github 仓库中获取。
通过测试很容易验证读取到的内容是正确的。接下来要完成的工作是:给定一个输 入任务(Batch)和一种排列组合(Perm),我们要计算出该组合所需的任务执行总时间(makespan)。
步骤1:计算加工时间(makespan)
如果按照常规做法的话,我们应该先自己手算出结果,再和测试结果相对比。但计算一个 20*5 的矩阵可不是那么好玩的。这里我用了一个取巧的办法:运行原程序,信任该程序的结果应该是正确的,用它来和本程序的输出对比。
运行原程序,输出类似这样(由于算法的不确定性,多次输入的顺序可能有所不同,但总时间应该相差不大)。完整的输出很长,这里只截取本步骤需要的关键部分:
Permutation: [15, 17, 14, 9, 8, 11, 13, 5, 3, 1, 19, 7, 16, 6, 18, 2, 4, 10, 20, 12]
Makespan: 1294
该输出显示了计算后得出的最优组合,且在该组合下的加工总时间是 1294。
我在阅读源代码之后观察到的一个规律:批次(batch,原文称为 data)和组合(perm)在代码中几乎总是一起出现的,也只有两者都确定之后才能得到一个有意义的结果。所以把它们组合起来作为一个对象是合理的,该对象我称为执行计划(Plan)。
按照结果编写测试如下:
class PlanTest(TestCase):
def test_makespan(self):
batch = reader.read_sample_batch()
perm = [14, 16, 13, 8, 7, 10, 12, 4, 2, 0, 18, 6, 15, 5, 17, 1, 3, 9, 19, 11]
plan = Plan(batch, perm)
self.assertEqual(1294, plan.makespan())
考虑一下如何计算任务的执行时间。前面已经介绍过,某个任务 i 开始执行必须满足两个先决条件:
- 同一批次的任务
i-1已经执行完毕; - 该任务所在的机器没有其他任务在执行。
因此,计算任务时间也需要按照从左到右、从上到下的顺序依次进行,先计算出其所依赖的上级任务时间,再计算该任务本身的时间。也就是说,要计算 task(i,j) 的开始时间,需要先计算:
task(i-1,j)开始时间 +task(i,j)执行时间task(i,j-1)开始时间 +task(i,j-1)执行时间
然后将两者之间的较大值作为本任务的开始时间(必须同时满足两个条件)。
如果读者去看原文代码的话,会发现作者是首先单独计算第一行和第一首列的数据,然后再依次计算其他节点。这是因为首行以及首列各自缺少一种上游节点,所以计算方法有种不同。但这样也使得总体算法看上去颇为复杂,理解起来也更为费劲。实际上只要理解了基本原则,其实所有节点是可以统一处理的,只要增加一个额外的约束:如果前驱节点不存在的话,则认为其结束时间为0。
依照此原理,可以先实现 Plan 的骨架:
class Plan:
def __init__(self, batch, perm):
self.batch = batch
self.perm = perm
self._times = None
self._makespan = None
def makespan(self):
self.calc()
return self._makespan
这里用到了延迟计算的思想,其实也是一种性能优化。在原文代码中,计算时间的函数叫做 compute_solution(),但是我观察到它在不同的地方被调用了多次,其实每次计算的结果应该是完全相同的。通过数据组合以及缓存计算结果,可以避免这种重复计算的开销,并提高性能。在后面我们还会看到其他的性能优化方法。
我们再定义两个辅助方法,分别计算任务的执行时间和结束时间,此外还有一个独立的函数返回矩阵的维度,它们有助于简化后续代码。实际上,这些函数是在实现主体算法之后通过重构提取得到的,不过它们都简单到只有一行代码,我就不再描述具体的提取过程了:
def shape(batch) -> (int, int):
return len(batch), len(batch[0])
class Plan:
...
def get_task_time(self, i, j):
return self.batch[i][self.perm[j]]
def get_end_time(self, i, j):
return self._times[i][j] + self.get_task_time(i, j)
再之后是整体的时间计算:
def calc(self):
if self._makespan is not None:
return
num_machines, num_tasks = shape(self.batch)
def get_time(row, col):
if row < 0 or col < 0:
return 0
return self._times[row][col] + self.get_task_time(row, col)
self._times = [([0] * num_tasks) for _ in range(num_machines)]
for i in range(num_machines):
for j in range(num_tasks):
self._times[i][j] = max(get_time(i - 1, j), get_time(i, j - 1))
self._makespan = self.get_end_time(num_machines - 1, num_tasks - 1)
以上代码用内部字段 _times 来记录所有任务开始时间的矩阵。当矩阵中所有任务都按照顺序计算完毕后,整体任务的总时间就可以从右下角的最后一个任务得到。
执行本步骤开头部分编写的单元测试,确保算法是正确的。既然能够对单个排列组合计算时间了,现在就可以着手编写整体处理过程,比较多个不同的排列组合并得到优化的结果。
步骤2:策略
在前面已经介绍过,流水线调度算法的核心就是所谓的“爬山”。所谓爬山,按照任务分解的原则,可以细化为以下过程:
- 从某个起点出发。这个起点在哪里并不重要,甚至可以是随机选择的;
- 找到与目前位置相邻的点。对于调度问题来说,所谓“点”就是各种排列组合方案,相邻的点可以理解为相似的排列。当然,我们需要定义何谓“相似”;
- 从多个可能的候选方案中寻找一个“更好”的方案。按照设计目标,更好就是指任务完成的总体时间更短;
- 将找到的方案作为新的起点,循环上述过程。只要遵照前述的原则,这个探索的总体趋势应该是不断“向上走”的。
当然,查找答案的总时间需要有所限制,计算几百个小时去找到一个最优解是不切实际的。此外我们也分析过,一味“向上走”的话,最终找到的点不一定是最理想的,所以只要有可能,我们也需要适当考虑探索其他的方向。
这里再引入几个术语,理解了它们有助于阅读接下来的代码。我们需要实现两套算法,分别对应于上述两个关键步骤:
- 查找邻接方案(
find_neighbors); - 选择邻接方案(
choose_neighbor);
这两个步骤组合起来构成了一套完整的寻路机制,我们把它叫做策略(strategy)。尽管策略的实现存在多种可能,但目前我们并没有足够信息能够预先断定哪种策略是最好的,因此本程序使用的是一种更为灵活的办法:实现多种不同的策略,在计算过程中记录哪种策略表现最好,并根据结果决定下一步的策略。
对于整个计算过程,我把它叫做问题(Problem)。Problem 的职责包括:
- 记录要处理的批次(
batch)作为输入 - 管理需要执行的策略
- 根据策略执行计算并得到结果(
solve),这也是整个过程最为关键的部分 - 输出结果
Problem 可以说是本文代码的顶层类了,尽管已经得到了大幅度的简化,但承担的职责决定了它初看起来还是有点复杂。为了清楚起见,下面列出的代码只包含核心逻辑,略去了一些相对来说不那么重要的部分:
class Problem:
def __init__(self, batch, time_limit):
self.batch = batch
self.time_limit = time_limit
self.strategies = StrategyList()
def solve(self):
num_machines, num_tasks = shape(self.batch)
# 初始排列随机
init_perm = list(range(num_tasks))
random.shuffle(init_perm)
best_plan = Plan(self.batch, init_perm)
while time.time() - start_time < self.time_limit:
strategy = self.strategies.pick()
candidates = strategy.finder(best_plan)
perm = strategy.chooser(best_plan, candidates)
curr_plan = Plan(self.batch, perm)
if curr_plan.makespan() < best_plan.makespan():
best_plan = curr_plan
...
print(f'Iteration {self.iteration}, progress {percent * 100:.1f}%, strategy: {strategy.name}...')
return best_plan
这里最关键的代码是关于选择和处理策略的部分,也就是以下三句:
strategy = self.strategies.pick()
candidates = strategy.finder(best_plan)
perm = strategy.chooser(best_plan, candidates)
它实现了我们前面描述的算法。当然,接下来需要实现策略,它目前是一个非常简单的聚合类:
class Strategy:
def __init__(self, name, finder, chooser):
self.name = name
self.finder = finder
self.chooser = chooser
查找邻居(find_neighbors)以及选择邻居(choose_neighbor)是两套算法,算法可以实现为函数。由于两套算法都存在多种候选方案,有些方案还比较复杂,所以我选择分步实现:先实现最简单和最基础的策略,让整个过程跑起来,后续再继续补充其他算法。
为了便于管理,我把算法部分实现为单独的包(algorithms),该包下又分两个模块,分别是 choose 和 find。每种候选算法作为模块中一个单独的函数。
随机生成邻接方案的算法很简单:对原组合调用 random.shuffle() 即可。但应该生成多少邻居呢?从职责划分的角度讲,算法应该只负责逻辑,而决策应交给上层调度者来决定。因此,该函数接受一个输入参数:
def rand(plan, num=1):
def shuffle_tasks():
perm = plan.perm[:]
random.shuffle(perm)
return perm
return [shuffle_tasks() for _ in range(num)]
至于随机选择邻居就更简单了:
def rand(plan, candidates):
return random.choice(candidates)
最后再实现一个对象,让它把多种策略统一管理起来,同时也让 Problem 类的工作变得更存粹一些。目前,我们只实现了单一的算法,但是既然已经知道未来还会有更多算法,那么接口可以设计为集合,让后续的添加变得更加轻松:
from .algorithms import find_neighbors as fn
from .algorithms import choose_neighbor as cn
class StrategyList(UserList):
def __init__(self):
finders = [
('Random Permutation', partial(fn.rand, num=100)),
]
choosers = [
('Random Selection', cn.rand),
]
strategies = [Strategy('%s / %s' % (fname, cname), f, c)
for fname, f in finders
for cname, c in choosers]
super().__init__(strategies)
def pick(self):
return random.choice(self)
请注意 pick() 方法:我们目前选择策略的方法也是简单粗暴地随机挑一个。这显然是不合适的,但这个工作还需要其他额外的信息,在该步骤中,我们希望首先让整个算法能够先跑起来,不要分心去处理其他目标。继续优化策略是后续两个步骤的任务。
实现上述代码后,我们可以跑一跑程序,确认整个计算是否可以正常工作:
def main():
batch = reader.read_sample_batch()
problem = Problem(batch, time_limit=10)
plan = problem.solve()
problem.dump(plan)
当然了,目前算法是完全随机的,所以每次输出的结果都会完全不同,得到的工作时间也并不理想。没关系,我们继续去完善它。
步骤3:复杂策略
在这个步骤中,我们会在随机方案的基础上,实现其他更多、也更复杂的查找/选择策略。
要获得“相邻”的方案,一个很容易想到的办法是,把排列组合中任意两个元素交换位置。这也是我们接下来要实现的算法,代码中叫做 swap。
from itertools import combinations
def swap(plan):
def swap_index(i, j):
perm = plan.perm[:]
perm[i], perm[j] = perm[j], perm[i]
return perm
indexes = range(len(plan.perm))
return [swap_index(i, j) for i, j in combinations(indexes, 2)]
以上算法和原文代码的实现是等价的,但风格上有所不同:原文基本上使用的是命令式的 for 循环风格,而我个人更加偏爱函数式的写法。对数组中元素的处理往往是复杂操作,不可能放在一行内,这种情况下我会引入一些内部函数,以保持代码主体的简洁。
上述代码也用到一个 Python 标准库内置、但日常很少会用到的函数:itertools.combinations。它在一个集合中返回指定数量的元素的所有组合————老实说,光看文字描述的话,我相信大多数同学应该和我一样觉得不好理解。好在它实际上也算不上复杂。在 REPL 下随便输入一些数字来验证,相信大家很快就能理解其含义了。后面还会用到另外一个函数:itertools.permutations,它的作用是返回指定集合的全排列。不必纠结于这些枯燥的文字描述,我们同样可以利用 REPL 来理解它的行为。
再下来的算法可以看作是 swap 的进一步泛化————不限于2个元素,而是 N 个元素的置换,从而使得尝试范围更加扩大。在原文中把这种算法叫做LNS(大邻域搜索 Large Neighbourhood Search)。但是,这也意味着候选方案的数量呈指数型上升。为了让搜索算法能够在有限的时间内得到结果,我们需要对搜索数量有所限制。
考虑到以后的算法也可能会需要,我增加了一个独立模块 params 来专门定义算法所需的参数:
MAX_LNS_NEIGHBORS = 100
然后实现算法:
def lns(plan, size=3):
candidates = []
indexes = range(len(plan.perm))
neighbors = list(combinations(indexes, size))
random.shuffle(neighbors)
best_plan = plan
for subset in neighbors[:params.MAX_LNS_NEIGHBORS]:
for ordering in permutations(subset):
if ordering == subset:
continue
perm = plan.perm[:]
for i in range(len(ordering)):
perm[subset[i]] = plan.perm[ordering[i]]
curr_plan = Plan(plan.batch, perm)
if curr_plan.makespan() < best_plan.makespan():
best_plan = curr_plan
candidates.append(best_plan.perm)
return candidates
由于涉及到多元素的处理,看起来有一点复杂。基本思路是从受限的子集中查找比当前方案更好(时间短)的那些作为候选方案。这里我增加了一点优化:由于 itertools.permutations() 返回的全排列是包含原始排列的,但原始排列就没有必要再去计算一次了,因此可以直接跳过。对于双层循环来说,这点额外的努力可以省掉不少额外的计算,是值得付出的。
最后一个查找算法有点特殊:它是根据目前方案的效果来查找后续方案。如果你认真看过前面 Plan 程序的输出结果,应该知道在机器和任务的数据中有一项叫做 Idle Time,它的计算方法是这样的:
Idle Time=(结束时间 - 开始时间) - 任务执行时间
也就是说,Idle Time 指的是机器没有工作、只是在等待前面的工序完成的时间。这个时间当然是越短越好。因此下面的算法名叫 idle,它的主要思想是找到那些等待时间最长的作业,调整它们的顺序,来看看是否能得到更好的结果。
def idle(plan, size=2):
candidates = []
stats = list(plan.job_stats())
stats.sort(key=lambda x: x[3], reverse=True)
subset = [x[0] for x in stats[:size]]
for ordering in permutations(subset):
if ordering == subset:
continue
perm = plan.perm[:]
for i in range(len(ordering)):
perm[subset[i]] = plan.perm[ordering[i]]
candidates.append(perm)
return candidates
在执行输出时,按照计算和显示分离的原则,我创建了一些辅助函数来进行计算,比如 job_stats() 方法用来计算作业的时间信息,其数据列包括作业序号、开始时间、结束时间以及 Idle time。该方法在这里也得到了重用:我们根据 Idle Time 来排序,再把对应的作业进行重新组合。究竟要取多少作业也是一个策略问题,我们把它作为输入参数,让调用者来决定。
选择邻居的算法只需返回一项即可,因此更加简单。目前我们已经实现了随机选择算法,接下来要实现的也很明确:选择所有候选项中时间最短的那个。
def hillclimbing(plan, candidates):
plans = [Plan(plan.batch, x) for x in candidates]
plans.sort(key=lambda x: x.makespan())
return plans[0].perm
当然,总是选择下一步“最优”的结果,无法保证最终得出的也是最优。既然我们无法预知哪条路径导向“最优”,那么只能通过尝试:在算法中加入一定随机性,来探索其他可能。以下就是爬山算法的一种变化,它的基本思想是在“比较好”的那些答案中,通过随机选择来探索其他可能的路径:
def random_hillclimbing(plan, candidates):
plans = [Plan(plan.batch, x) for x in candidates]
plans.sort(key=lambda x: x.makespan())
subset_size = int(len(plans) / 2)
subset = plans[:subset_size]
return random.choice(subset).perm
现在,我们拥有了多种查找和选择算法,只要把它们加入策略集合即可。不过,某些算法是需要额外参数的。为了让主程序能够以统一的方式调用各种策略,我们用柯里化去除额外参数,统一策略的对外接口。对于 LNS 算法而言,我们也并不知道究竟调换多少元素效果才好,所以不妨多尝试几种可能:
from functools import partial
class StrategyList(UserList):
def __init__(self):
finders = [
('Random Permutation', partial(fn.rand, num=100)),
('Swapped Pairs', fn.swap),
('Large Neighbourhood Search (3)', partial(fn.lns, size=3)),
('Idle Neighbourhood(3)', partial(fn.idle, size=3)),
('Idle Neighbourhood(4)', partial(fn.idle, size=4)),
('Idle Neighbourhood(5)', partial(fn.idle, size=5)),
]
如果你去看原程序的话,会发现作者还有一个策略是 LNS(2)。我在测试时发现,因为两个元素互换位置只有一种变化,所以 LNS(2) 其实就是 swap,没有必要多做一次,因此把这个策略去掉了。
现在我们实现了所有策略,但算法还差最后一步。回忆一下 StrategyList.pick(),它的实现目前是从众多策略中随机选择一个。在下个步骤种,我们将实现策略的动态选择。
步骤4:动态选择策略
对于策略的选择而言,原文所使用的方法也是很有趣的。它首先为所有策略分配一个权重(weight),所有权重一开始都是 1,这意味着它们被选中的机会是均等的。但在每计算一个新的组合之后,会记录两个统计数字:计算该组合所需的时间,以及该组合在总体运行时间上的变化(可能为正也可能为负)。工作时间更短或者运行时间少都认为是“更好”的,也就是对该策略加分。在运行一定时间之后,根据各个策略的权重变化重新排序,并优先选择那些过去一段时间表现更好的策略。
以上是选择策略的总体原则。该算法也考虑到一个因素,即:如果某些策略如果从来没有被使用过,那么它们的评分没有变化,也无法得到“露脸”的机会,这种情况是应当避免的。因此,作为一种补偿,该算法也会给那些没有使用过的算法一个较大的加分,以使得下一次它们有更大的概率被选中。
思路明确了,代码也就好写了。首先我们给策略添加一些记录统计信息的字段,以及更新统计信息的方法:
class Strategy:
def __init__(self, name, finder, chooser):
...
self.usage = 0
self.improvements = 0
self.time_spent = 0
self.weight = 1
def update_usage(self, time_spent, improvements):
self.usage += 1
self.time_spent += time_spent
self.improvements += improvements
然后,在运行时记录并更新统计信息(只列出修改部分):
class Problem:
def solve(self):
...
start_time = time.time()
best_plan = Plan(self.batch, init_perm)
while time.time() - start_time < self.time_limit:
iteration_start_time = time.time()
...
time_spent = time.time() - iteration_start_time
improvements = best_plan.makespan() - curr_plan.makespan()
strategy.update_usage(time_spent, improvements)
...
if (self.iteration % params.STEP_ITERATIONS) == 0:
self.strategies.update_stats()
...
return best_plan
update_stats() 方法的主要工作是:基于上一次迭代的统计数字重新计算权重,并把原先的统计数字清零(每次迭代的统计信息并不累计)。我们还会看到,没有被调用的策略会赋予更大的权重:
def update_stats(self):
strategies = self.copy()
strategies.sort(key=lambda x: x.improvements, reverse=True)
for index, s in enumerate(strategies):
if s.time_spent > 0:
s.weight += len(strategies) - index
else:
s.weight += len(strategies)
s.improvements = 0
s.time_spent = 0
然后,根据统计信息选择下一步的策略:
def pick(self):
strategies = self.copy()
strategies.sort(key=lambda x: x.weight, reverse=True)
subset_size = int(len(strategies) / 3)
subset = strategies[:subset_size]
return random.choice(subset)
该算法也有一定随机性:它只选择过去一次迭代种权重较高的那些策略,但并不一定是选择最高的,而是随机选择,这样可以保证多种策略都有被执行以及重新评估的机会。
上述修改全部完成后,我们可以再次运行程序,确认输出结果是有效的。
步骤5:缓存优化
到此,我们算法的整体工作已经完成了。但我还希望对程序做一点改进,主要是在性能方面。
在阅读原程序时我注意到:该程序使用了过程式的方法,且基本上不记录中间状态。这样虽然使得程序简单、存粹,但明显有一些计算是被浪费了。比如说,执行组合需要的时间在循环时计算了一次,在输出时又计算了一次,显然它们的结果是相同的,没有必要重复执行。此外还可以设想,当使用各种不同策略时,它们返回的候选项也是有可能重复的。相同的排列组合应该总是返回相同的执行时间,再重复计算也是浪费。这些低效的重复计算有没有可能避免呢?
我们知道,一般来说,性能优化通常会让代码变得更加复杂,还有可能带来潜在的缺陷,因此最好是谨慎地引入它们,并且应该基于实测的性能数据,不要凭空猜测。但是对于此问题而言,优化方向相当简单而明确:对于相同的排列组合,它总是生成固定的结果。因此,我们可以使用一个字典作为缓存,其中排列组合作为字典的键,计算结果作为字典的值。如果该组合已经计算过,则直接从缓存中获取最终结果,不需要再次计算。
缓存是一种用空间换时间的策略,使用它可以加快速度,但代价是需要占用大量内存。如果缓存命中率不高的话,那么引入它就是得不偿失的。因此,要知道缓存的使用是否有效,我们还要记录它的命中率(Hit Rate)究竟如何,并作为一项统计信息包含到输出结果中。
设计数据结构如下:
class PlanCache:
def __init__(self, batch):
self.batch = batch
self._cache = {}
self.use_count = 0
self.hit_count = 0
def __getitem__(self, perm):
self.use_count += 1
key = tuple(perm)
if key in self._cache:
self.hit_count += 1
else:
plan = Plan(self.batch, perm)
self._cache[key] = plan
return self._cache[key]
def dump(self):
hit_rate = self.hit_count / self.use_count
print(f'Cache usage: Used {self.use_count} times, Hit Rate={hit_rate * 100:.1f}%')
在前面的代码中,我们把排列组合记录为列表(list)类型。但是在 Python语言中,包含列表在内的可变数据类型不能作为字典的键,所以在加入缓存之前需要先做个转换,把它变成不可变的 tuple。
然后,修改计算过程:
class Problem:
def __init__(self, batch, time_limit=10):
...
self.cache = PlanCache(batch)
def solve(self):
...
while time.time() - start_time < self.time_limit:
# origin: curr_plan = Plan(self.batch, perm)
curr_plan = self.cache[perm]
这里的修改是很容易的。棘手的地方在于部分策略也需要计算 Plan,为了让它们也能避免重复计算,我们把所有策略增加一个上下文参数,它其实就是 Problem 自身(因为 Problem 才持有缓存)。这样,策略也可以使用缓存了。
修改 Problem 的计算过程,让策略的调用增加一个额外的参数,这里叫做 ctx:
strategy = self.strategies.pick()
candidates = strategy.finder(self, best_plan)
perm = strategy.chooser(self, best_plan, candidates)
然后,为所有策略函数添加 ctx 参数,并检查它们是否在内部创建了 Plan,如果有则替换为对缓存的调用。比如,LNS 策略修改如下:
def lns(ctx, plan, size=3):
...
for subset in neighbors[:params.MAX_LNS_NEIGHBORS]:
for ordering in permutations(subset):
...
# origin: curr_plan = Plan(plan.batch, perm)
curr_plan = ctx.cache[perm]
...
candidates.append(best_plan.perm)
return candidates
这些工作完成之后,我们可以运行修改前后的程序,对比看看它们的性能变化。在我的机器上,修改之前运行结果类似这样:
Went through 13994 iterations.
添加缓存之后:
Went through 164759 iterations.
Cache usage: Used 40980437 times, Hit Rate=97.4%
由此可见,缓存利用率是相当高的,且迭代时间也得到了明显的缩短,说明这种优化是有意义的。如果效果不佳的话,则应当把缓存去掉,不必让代码变得无谓地复杂。
总结
在本文中,我们以自己的方式重新实现了一种典型的流水线调度算法。尽管这个算法还是比较简化的,但足以让我们接触到动态规划的一些主要概念、思路和算法。同时,也有机会接触到 Python 标准库中比较鲜为人知的一些集合算法。
和原文程序相比,本文程序最大的改变应当说是大量使用了 OOP 的设计思路,把不同的职责分类管理起来。通过以上各个迭代过程,这种划分的确是有益的:我们基本上可以每次把修改范围聚焦在一两个类范围内,不必担心造成全局的影响。当然,这也是建立在对于算法有一个清晰的理解基础上的。
本程序相对于原程序而言的另一处改进是有意识地进行性能优化,避免不必要地重复计算,以提高性能。这是原程序不太注重的地方。从最后一步的结果可以看到,这种重复计算还是相当普遍的,有很大的提升空间。对于题目涉及的二维数组计算(相应的在算法上需要双层循环),哪怕一点优化也能产生显著的效果,是值得付出额外努力的。当然,我们还是需要一些明确的行呢个评估指标来确定优化是否真的有意义。
如果想要进一步优化算法效率的话,一个可能的方向是引入并行计算。但对于该算法而言,由于需要根据度量数据去调整策略,这些中间数据的存在使得计算过程是上下文相关的,从而要实现并行有一定难度,且会显著增加代码的复杂性。如果读者有兴趣的话,不妨自己去挑战一下。
动态规划是一个复杂的数学问题,原文提出的问题也是一个经过简化的、比较纯粹的数学问题,现实中的规划问题往往要复杂得多。如果读者对这个领域感兴趣的话,原文也提供了一些额外的信息和阅读材料,有兴趣的读者也可以自行阅读。
文章索引
- 重写 500 Lines or Less 项目 - 前言
- 重写 500 Lines or Less 项目 - Web Server
- 重写 500 Lines or Less 项目 - Template Engine
- 重写 500 Lines or Less 项目 - Continuous Integration
- 重写 500 Lines or Less 项目 - A Simple Object Model
- 重写 500 Lines or Less 项目 - A Python Interpreter Written in Python
- 重写 500 Lines or Less 项目 - Contingent
- 重写 500 Lines or Less 项目 - DBDB
- 重写 500 Lines or Less 项目 - FlowShop
- 重写 500 Lines or Less 项目 - Dagoba
- 重写 500 Lines or Less 项目 - 3D 建模器